Texas Hold'em Math 10
Shortcuts For Calculating Odds
OK, so now you know the details of "poker math" and how to calculate pot odds… while also taking implied odds and appropriate adjustments into consideration.
Up until this point we've been using the CHARTS as our source of data. Now I want to teach you how to use the odds WITHOUT charts… and without complicated calculations. This will give you the power to understand in-depth poker math IN YOUR HEAD… without being a math genius.
OK, let's get started.
First off, let me show you a neat shortcut, based on the percentage charts. Here is the chart again:
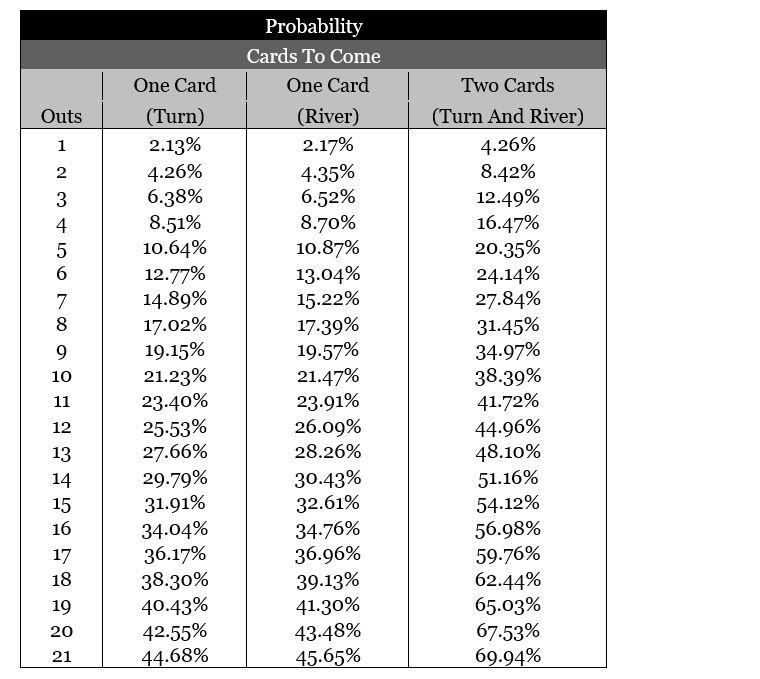
As you know, it's not really necessary to know the EXACT percentage. For instance, 2.13% can be considered 2%, 6.38% can be considered 6%, 27.66% can be considered 28%, etc. for all practical purposes.
With that being said, you'll notice that you can find the percentage by DOUBLING THE OUTS and adding ONE. The "formula" looks like this:
(OUTS X 2) + 1 = % of getting a card you need
That formula works anytime you have between three and eleven outs. If you have FEWER than three outs, it doesn't really matter… since you should fold anyway. And if you have MORE than eleven outs, you've got great odds and will probably call (or raise).
To be exact, here are the formulas to cover the possibilities:
- 1-3 Outs: Outs x 2 = % of hitting
- 3-11 Outs: (Outs x 2) + 1 = % of hitting
- 12+ Outs: (Outs X 2) + 2 = % of hitting
For instance, let's say you pick up an open-ended straight draw and have eight outs. Instead of using the chart to find the percentage chance of hitting on the turn (17.02%), you can simply do it in your head. All you do is multiply eight by two and add one, which equals seventeen.
(8 outs x 2) + 1 = 17% Simple huh?
This is a very powerful strategy. For most real-life poker situations, you will have between three and eleven outs. And in most real-life poker situations you definitely won't have access to any charts. This makes the simple "double the outs and add one" technique easy-to-remember and quite efficient.
Of course, now the question becomes: How can this be used for POT ODDS?
As we discussed earlier, pot odds are found by comparing the hand odds in X:X format versus the betting odds in X:X format. If you're getting lots of money for a little investment, then a call is justified. To be exact… if the betting odds number is BIGGER (when in X:1 format), you should call. If it's smaller, you should fold.
For example…
If you're getting 4:1 on your money and 2:1 on your hand, a call is JUSTIFIED.
If you're getting 4:1 on your money and 8:1 on your hand, a call is UNJUSTIFIED.
OK, but now we have a problem. Before, we were using the charts for the X:X number… under the "odds against" column. How can we do the odds IN OUR HEAD and still use the SHORTCUT method we just discussed?
The solution is to CONVERT THE BETTING ODDS TO A PERCENTAGE. There are a few different solutions actually, but this is fastest and easiest.
What I mean is… instead of comparing everything in X:X format, we'll start comparing everything in terms of percentages.
All right, let's look at how to calculate the "betting percentage"…
We need the same two numbers as before: pot size and bet size. Before, we compared the numbers like this:
Pot Size: Bet Size
So if there was $100 in the pot and the action was to you to call a $20 bet, the figure would be 100:20, or 5:1.
Now all we want to do is CONVERT THAT into a PERCENTAGE. It's actually very easy. All we do is DIVIDE THE BET SIZE by the POT SIZE ADDED TO THE BET SIZE. The formula looks like this:
Bet Size / (Pot Size + Bet Size)
In our example before, the bet size was $20 and the pot size was $100. Plugging that into our formula…
20 / (100 + 20)
Which equals… 20/120
Which equals 1/6
You'll notice that 5:1 can be converted to 1/6 fairly easily. All you have to do is add five and one and make it the bottom part of the fraction. This is just another way to say the same thing as what we just did.
Then, your job is to know what 1/6 equals. This is the "hardest" part. If you're terrible at math, you can brush up on basic fraction percentages here:
- 1/2 = 50%
- 1/3 = 33%
- 1/4 = 25%
- 1/5 = 20%
- 1/6 = 16.5%
- 1/7 = 14%
- 1/8 = 12.5%
- 1/9 = 11%
- 1/10 = 10%
- 1/11 = 9%
- 1/12 = 8%
So for our example, we can see that 1/6 equals 16.5%.
The next step is to simply compare the BETTING PERCENTAGE with our HAND ODDS percentage. The hand odds are figured using the shortcut we just learned.
If the hand odds percentage is bigger than the betting percentage, a call is justified. If not, a call is unjustified.
| Hand % > Betting % | Call is justified. |
| Hand % < Betting % | Call is unjustified. |
All right, you're ready for a real-life example…
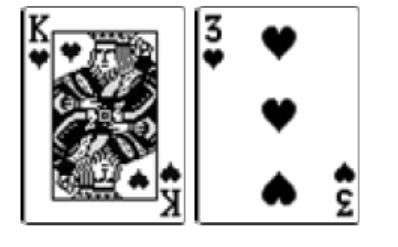
You get dealt:
The flop hits:
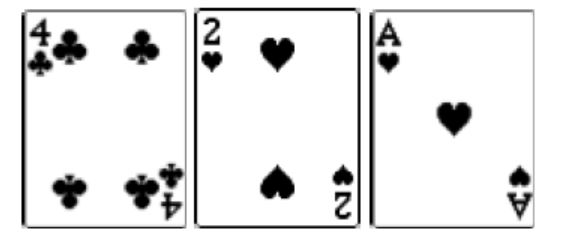
That means you have the nut flush draw with your four hearts.
You're on the button. There's $80 in the pot from before the flop. Sally bets $40 after the flop and three players call. The action is to you.
First, you calculate the pot size. It equals $240. You need to decide whether a call is justified or not. You have nine outs (since there are thirteen hearts in the deck and you already see four of them).
Plugging the nine outs into our formula…
(9 x 2) + 1 = 19%
If we were using the chart we'd see the actual percentage is 19.15%.
Now you must find the betting percentage. Since the pot size is $240 and the bet size is $40, we plug these numbers into our formula…
40 / (240+40) = 40/280 = 1/7
Now we just need to decide is 1/7 is bigger or smaller than 19%. Well, 19% is about 20%. So is 1/7 bigger or smaller than 20%? The answer is smaller.
That means that a call IS justified.
Of course… we haven't considered other factors in our example here. Since there were so many players in the hand, we would have DISCOUNTED a couple of the outs, since someone else was probably on the flush draw. BUT, we would have also considered the IMPLIED ODDS of busting someone else's flush with our "nuts".
So all in all, a call is a good decision to make either way you look at it. Let's do another example:
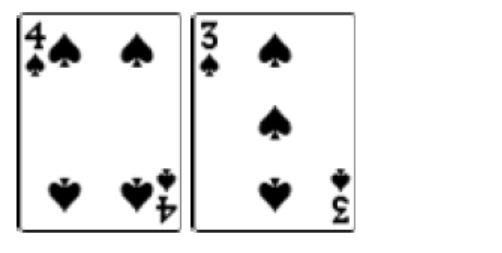
Say you get dealt:
The flop hits:
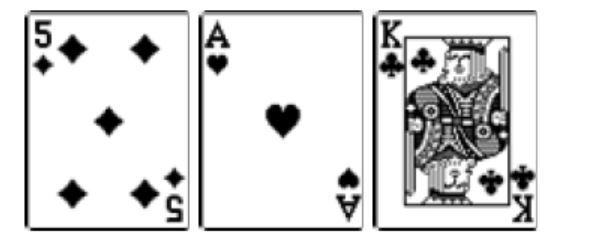
You've got an inside straight draw (you need a two). Let's say the pot size is $100 and the betting amount is $20. Should you call or fold? Well, since there are four twos in the deck, you know that you have four outs. After doubling that and adding one you have a 9% chance of making your straight on the turn.
Now you just need to decide if the betting percentage is larger or smaller. Divide 20 by (100 + 20). The answer is 20/120, or 1/6. You know that equals about 16.5%... so it's LARGER than 9%. That means your hand percentage is SMALLER.
Remember…
| Hand % > Betting % | Call is justified. |
| Hand % < Betting % | Call is unjustified. |
So in this case, you should FOLD.
A lot of this will become instinctual and "second nature" very soon. As you become familiar with these types of calculations, you'll understand that inside straights are hardly EVER worth chasing. It's the same way with staying in a hand just because you have one overcard… it's just not worth it.
Let's summarize the pot odds calculations one more time in this easy three-step process:
- Double your outs and add 1. This equals your approximate percentage of making your hand. (Your "hand odds percentage".)
-
Divide the bet size by the pot size added to the bet size. (This equals your "betting percentage".)
Bet Size / (Pot Size + Bet Size) - Compare the "hand odds percentage" to the "betting percentage". If the hand odds are higher, a call is justified. If the hand odds are smaller, a call isn't justified.
All that's left is to consider your implied odds, discounted odds, and make adjustments according to the players you're up against. If anything extreme sticks out (i.e. drawing for the nuts, up against a rare playing style, etc.), then you should factor that into your decision.
