Texas Hold'em Math 07

Calculating Implied Odds

Put simply, implied odds has to do with the "extra" amount of money you stand to win if you complete your hand (make your outs).

We'll start with an example. Let's say you're on the flush draw after the turn and have a 20% of making a winning hand (4:1). Your opponent has two pair. The action is to you to call a $20 bet. There's a pot size of $70.

In terms of "explicit odds" (what we've been doing so far), you know that in order make a justified call there needs to be at least $80 in the pot… but there's only $70.

But in this situation, your opponent has been betting aggressively the entire hand. You're confident that he'll bet again after the river no matter what hits… and that you'll be able to even RAISE him for more money.

You figure you can get at least another $30 from your opponent if you hit your flush. So you add this "implied value" to the current pot size… and see that it's worth calling now.

That's how implied odds work. There's no "math" to them, because they're based on your intuition. They aren't present in every hand situation—just the ones where you have a "hidden" hand or your opponent is too pot-committed, etc. Considering implied odds requires that you have a read on your opponents and can roughly deduce what they're holding.

The implied value of an out is up to you. The great thing about no limit Holdem is that often the implied value is DOUBLING UP. If you hit a hidden hand on the river, you can get your opponent to call an all-in bet and take every single last one of his chips.

For instance, here's a cool scenario. Let's say you've got pocket Aces:

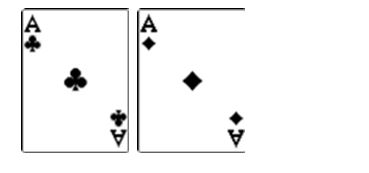
The board reads:

Your opponent has:

That means your opponent has the flush and you have trip aces. There's just one river card left to go. Your opponent (who is chip leader) bets $2,800 into a $800 pot.

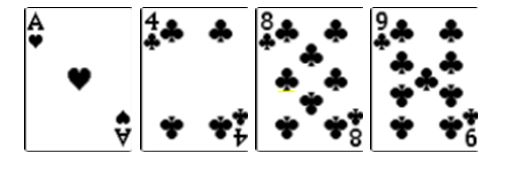
You have lots of outs here. There's:

1 ace + 3 fours + 3 eights + 3 nines + 7 clubs left = 20 outs

The fours, eights, and nines give you a full house. The other club would give you the nut flush. With twenty outs, the explicit odds STILL don't quite justify a call. But you know that if you DO get your full house or nut flush, you'll be able to move the REST of your chips into the middle and double up.

You'd factor a lot of different things into this type of decision, including the implications of LOSING all your money (Is it a tournament or cash game? Are there re-buys?), how big your chip stack is, how many players are at the table, and so on.

This is an extreme example, but it shows the importance of implied odds. Most all-in decisions are made according to implied odds, which is part of the reason why the behavior from one card player to the next is so different.

All right, let's move on to "discounted odds".