mttsports
MTTSports | Guide | News

Playing Texas Hold'em Online, The Professional Guide - Chapter 4-1

Everything You Always Wanted to Know (And Maybe Didn't) About Odds, Permutations and Return on Investment

WHAT ARE CARD ODDS?

If you haven't already noticed, probability is a huge factor in Texas Hold'em. For example, there are 2,598,960 possible hands in a 52‐card deck but only 4 Royal flush. If the average serious poker player is dealt 100,000 hands in their lifetime, they will never hold (on the first five cards) more than 4 percent of all the possible hands. And likely a lot less.

Figuring out straight card combinations for the purpose of this text are called Card Odds (you will be introduced to other kinds of odds later). Card Odds can reveal some quite interesting information.

For example, how many pat straight flush will you see in your lifetime? To determine that number, the expected number of hands that could be dealt during your lifetime is estimated by the following calculation:

10 complete poker hands / hr. x 5 hrs. / game x 50 games / yr. x 40 yrs. / poker life = 100,000 hands of poker per lifetime.

This is a pretty aggressive estimate, as most people will never come close to this number of complete hands in Texas Hold'em. Based on this level of play, the number of pat (on the first five cards) poker hands that you should get during your lifetime is calculated from the card odds and tabulated as follows:

Cards Dealt Number of Pat Hands

So statistically, you should see a pat straight flush on your first five cards once or twice during your lifetime. Most average poker players will never see even one.

Card players often talk about having a 'lucky streak' or a 'run'. Mathematically, 'streaks' don't exist. But suppose you did have an amazing run of cards one evening. What would the odds be of having five consecutive straight flush in a row?

Hand Ways to Make Probability
Royal Flush 4 .0000015391
Other Straight Flush 36 .0000138517
Four of a kind 624 .0002400960
Full House 3,744 .0014405762
Flush 5,108 .0019654015
Straight 10,200 .0039246468
Three of a kind 54,912 .0211284514
Two Pairs 123,552 .0475390156
One Pair 1,098,240 .4225690276
Nothing 1,302,540 .5011773940
Total 2,598,960 1.0000000000

In every 1.7x1024 deals . . . or once in every 700,000,000,000,000,000,000 years. You'd have to read those cards in the dark though, because our sun will be long gone by that time.

Players use card odds to make playing decisions. A decision made without taking into account card odds makes poker a guessing game. The chances of finishing a flush or a straight, the probability of getting an over card (face card), the percentage of times you're going to flop a card to match your pocket pair are all extremely important factors in Texas Hold'em.

Knowledge of these statistics is key to winning.

Here are some other basic probabilities that you should know about:

HOW ARE THE ODDS CALCULATED?

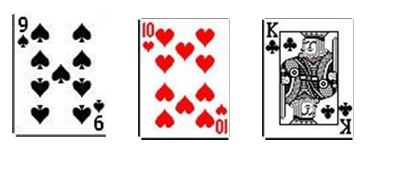
Let's look at the example of having 4 outs (four cards you need to make your hand). Say you're holding 6c 7d and the flop comes 9s 10h Kc. In this case you need an 8 to make the straight. Since there are four 8's in the deck, you have 4 outs.

YOUR POCKET

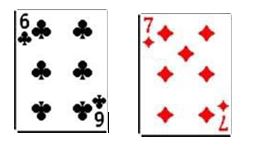
Play Texas Holdem Online Professional Guide 004

THE FLOP

Play Texas Holdem Online Professional Guide 004

ODDS WITH ONE CARD TO COME

Calculating the odds with one card to come is relatively straightforward.

When you're looking to make the inside straight, you have four outs. There are a total of 46 unknown cards (52 minus the 2 cards in your hand minus the 3 cards for the flop and the 1 turn card). 42 of the cards don't make your hand and four do. 42:4 or 10.5:1 = about 9%. I prefer to use the percentage as it helps when calculating Pot Odds (to come later).

ODDS WITH TWO TO COME

To calculate the appropriate odds with two cards to come, you must first determine the total number of two‐card combinations possible after the flop.

The easiest way to calculate this is by multiplying the number of cards available for the turn (47) by the number of cards available for the river (46) and dividing that number by 2 (because a card can't match itself). 47*46/2 = 1081.

A certain number of these 1081 two‐card combinations will have eights in them. To determine odds properly, you need to calculate two more figures.

EIGHTS ON BOTH THE TURN AND THE RIVER

One of the four eights can appear on the turn. And if one does, there will be three lefts for the river. If you multiply 4 by 3 and divide by 2 (because a card can't match itself) you see that there are six unique pairing of 8s.

EIGHTS ON THE TURN OR RIVER

If an eight comes on the turn, there are 46 unseen cards remaining. But you're no longer interested in the three remaining eights, so, you can subtract those. This leaves 43 unseen cards that will make e a unique pair with one of the eights. Multiply 4 (the number of 8s in the deck) by 43 (the number of unseen cards) to arrive at 172.

FINISH THE CALCULATION

172 plus 6 comes to 178 ‐‐ the total number of two‐card combination that has at least one eight in them and as many as two eights.

Out of 1081 possible two‐card combinations on the turn and river, 178 of those combinations help us make our hand. Subtract 178 from 1081 to find the number of combinations that don't make the straight (1081‐178=903).

The odds against making a straight by the river are: 903:178, or 20%.

What About The Cards The Other Players Are Holding?

Ever wonder why we never factor the opponents' cards or the burn cards when figuring out how many cards are left?

The reason is that we only consider unseen cards. If you saw what the burn cards were, or an opponent showed you his hand, you would know that those cards are not going to be drawn and could use that. We typically do not know what they have, so we don't even think about it when talking about odds.

For instance, take a standard deck of 52 cards, remove 2 Aces and burn 25 of them. If you drew the next card, what are the chances of it being an Ace? It would be 2/50 (2 Aces left out of 50 unseen cards). It would NOT be 2/25 just because you burned half the deck. Okay, do the same thing again, but this time you get to look at the burn cards. Let's say that of all the cards you burned, none were an ace. Now your odds are 2/25 because there are still 2 Aces and now only 25 "unseen cards".

You will find that you can easily remember a few of the most common situations for outs such as the four flush or straight draw but there has to be an easier way than memorizing the figures for every number of outs. The good news is that there is a way to get a good estimation of the odds without the heavy math and you can also use handy odds charts.

WHAT HANDS WILL WIN THE POT?

The following are the most valuable starting hands in Texas Hold'em. This chart assumes a medium to lose $5‐10 Texas Hold'em game. The results are based on a computer simulation of 5,000,000 played hands. The percentage shown indicates how many times in typical game that these hands win the pot.

This is interesting data – but here's the kicker – look at the power of two pairs and single pair hands. It's not only higher than the WHAT ARE MY CHANCES OF WINNING?

What are my chances of winning a hand with a given set of pocket cards? What are the odds of filling a straight?

Play Texas Holdem Online Professional Guide 004

How much you can expect to profit from these starting hands?

The starting hand average win for each time played based on medium to lose Texas Hold'em Poker games with a $5/$10 limit.

POCKET CARD ODDS

Hole Cards Odds

After the Flop

The River (5th Street)

More Interesting Texas Hold'em Odds

WHAT ARE POT ODDS?

Pot odds are the odds you get when analyzing the current size of the pot vs. your next call or bet. Pot Odds help you make important call, raise or fold decisions.

Example 1: There is $200 in the pot and a final $10 bet coming at you. You are looking to fill in your 4‐card flush. Based on needing one of four suits, the short‐cut math is 1:4 chances or 25%. Winning consistently is about beating Pot Odds and not over‐betting. If your Card Odds are 25% (you have four hearts and need another to win) and you only need to bet 5% of the present pot ($10 as a percentage of the $200) to see the last card, you are in great shape. Based on Pot Odds for this hand you could go as high as 25% of the pot based on your odds to pull a heart on the river.

Play Texas Holdem Online Professional Guide 004

Example 2: You are in a $5/$10 Hold'em game with Jack‐Ten pocket cards and one opponent left on the turn.

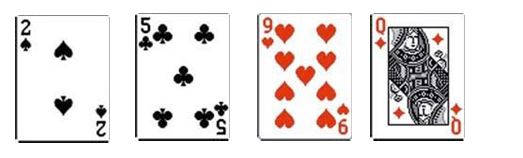
Play Texas Holdem Online Professional Guide 004

You have an outside straight draw with a board of 2‐5‐9‐Q, and only the river card left to make your straight. Any 8 or any King will finish this straight for you, so you have 8 outs (four 8's and 4 K's left in the deck) and 46 unseen cards left. 8/46 gives you a 6:1 chance or a 17% chance of getting the win. Your opponent bets$10.

6/1 = 17% Pot Odds

If you take a $10 bet you could win $100. Your bet is then 10% of the final pot. The 10% bet is smaller than the 17% odds, so you are in good shape from an investment point of view.

Whenever your call or bet (in this case 10% of the pot) is smaller than your odds of getting the winning hand (17%) you are buying the next card at a discount. The key is looking at the odds of a winning hand, not building a part of a winning hand.

Too many beginners just play good cards and just toss bad ones or if they have the prospect of straight or a flush they will just draw and draw with little consideration to anything else.

Unless you have the NUTS (nuts = the very best possible hand) every time there is a certain degree of risk when you put your money in the pot.

In the heat of the battle, you may not always have time to get out your calculator and do the number crunching .You can look at Pot Odds in a much simpler way ‐ just ask yourself if there is enough money in the pot to justify the risk?

If there is a big pot ‐ unless you just know you are beat, or it simply costs too much to call (which means your pot odds may not be so great after it's all said and done) ‐ try to get some action. Even if you knew you were a long shot ‐would you bet $25 or $50 on a chance to win $500 or $1000 or more? While you may be a long shot ‐ it's not a bad bet if there is a reasonable chance you could win.

On the flip side, and this is important, you may have a decent hand and it may even be the winner, (use your opponent or 'tells' knowledge) but if it's going to cost you $250 to call and you stand to only win a few hundred then your pot odds are not so great and is probably not worth the risk.

Pot odds ratios are a useful tool to see how often you need to win the hand to break even.

If there is $100 in the pot and it takes $10 to call, you must win this hand 1 out of 11 times in order to break even. The thinking goes along the lines of: If you play 11 times, it'll cost you $110, but when you win, you get $110 ($100 + your $10 call).

The usefulness of card odds and pot odds becomes very apparent when you start comparing the two. As we know now, in a flush draw, your card odds for making your flush are 1.9 to 1 or 35%. Let's say you're in a hand with a nut flush draw and it's $5 to you on the flop to call. Do you call? Your answer should be: What are my pot odds?

If there is $15 in the pot plus a $5 bet from an opponent, then you are getting 20:5 or 4:1 pot odd –25%. This means that in order to break even, you must win 1 out of every 5 times. However, with your flush draw, your odds of winning are 1 out of every 3 times! You should quickly realize that not only are you breaking even, but you're making a nice profit on this too. Let's calculate the profit margin on this by theoretically playing this hand 100 times from the flop, when is then checked to the river.

Total Cost to Play = 100 hands * $5 to call = ‐$500

Pot Value = $15 + $5 bet + $5 call = $25

Odds to Win = 1.9:1 or 35% (From the flop)

Total Hands Won = 100 * Odds to Win (35%) = 35 wins

Net Profit = Net Cost to Play + (Total Times Won * Pot Value)

= ‐$500 + (35 * $30)

= ‐$500 + $1,050

= $550 Profit

As you can see, you have a great reason to play this flush draw, because you'll be making money in the long run according to your card odds and pot odds. The most fundamental point to take from this is:

If your Pot Odds > Card Odds, then you are making a profit.

So, even though you may be faced with a gut shot straight draw at times, which is a terrible draw at 5 to 1 hand odds, it can be worth it to call if you are getting pot odds greater than 5 to 1. Other times, if you have an excellent draw such as the flush draw, but someone has just raised a large amount so your pot odds are 1:1 for instance, then you obviously should not continue trying to draw to a flush, as you will lose money in the long run. In this situation, a fold or semi‐bluff is your only solution, unless you know there will be callers behind you that improve your pot odds to better than break even.

Your ability to memorize or calculate your card odds and figure out your pot odds will lead you to make many of the right decisions in the future. Just be sure to remember that fundamental principle of playing drawing hands when your pot odds are greater than your card odds.

Another good rule to follow ‐ a lot of players want to somehow factor in money they wagered on previous rounds. With the last example, you probably had already invested a significant portion of that $200 pot. Let's say $50. Does that mean you should play or fold because of that money you already have in there? $50/$200?

That's a big no.

That's not your money anymore! It's in a pool of money to be given to the winner. You have no stake in that pot. The only stake you might have been totally mental and has no bearing on hard statistics.

The next step is to use bet odds and implied odds. That's tougher, because it involves predicting reactions of other players. With bet odds, you try to factor in how many people are going to call a raise. With implied odds, you're thinking about reactions for the rest of the game. One example on implied odds . . .

Say it's another $5/$10 Hold'em game and you have a four flush on the flop.

Your neighbor bets, and everyone else folds. The pot is $50 at this point. First you figure out your chance of hitting your flush on the turn, and it comes out to about 19% (about 1 in 5). You have to call this $5 bet vs. a $50 pot, so that's a 10x payout. 1/5 is higher than 1/10, so bet odds are okay, but you must consider that this guy's going to bet into you on the turn and river also. That's the $5plus, two more $10 bets.

So now your facing $25 more till the end of the hand. So, you have to consider your chances of hitting that flush on the turn or river, which makes it about 35% (better than 1 in 3 now), but you have to invest $25 for a finishing pot of $100. $100/$25 is 1 in 4. That's pretty close.

But there's more!

If you don't make it on the turn, it'll change your outs and odds! You'll have a 19.6% chance of hitting the flush (little worse than 1 in 5), but a $20 investment for a finishing pot of $100! $100/$20 is 1 in 5. So, the chances could take a nasty turn if you didn't hit it! What's makes it more complicated is that if you did hit it on the turn, you could raise him back, and get an extra $20 or maybe even $40 in the pot.

Once you've mastered simple outs and pot odds, bet and implied odds are just a longer extension of these equations. If you think about these things while you play, they will eventually become second nature to you.

More Odds Examples: A pocket pair

You start with a pair of Jacks in the pocket. Not too shabby. The flop however, doesn't contain another Jack.

YOUR POCKET

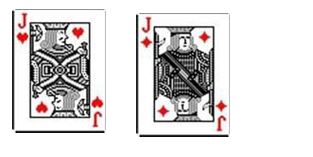
Play Texas Holdem Online Professional Guide 004

THE FLOP

Play Texas Holdem Online Professional Guide 004

Example #2 "The straight draw"

THE POCKET

Play Texas Holdem Online Professional Guide 004

You start with a Jack of Spades and a Ten of Spades. You get a rainbow flop with a Queen of Spades, a Three of Diamonds, and a Nine of Clubs. You've got a straight draw.

THE FLOP

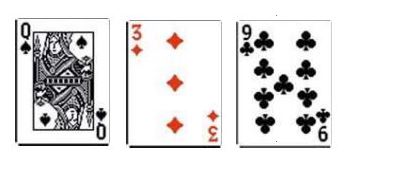
Play Texas Holdem Online Professional Guide 004

Lesson 1:

Play Texas Holdem Online Professional Guide 004

THE FLOP

Play Texas Holdem Online Professional Guide 004

Once again, we'll have to calculate the chances of a King or Eight NOT appearing, so we can do it like the last problem (in this case, {39/47} X {38/46}). Or, since we've already figured out our chances in the previous two lessons, we can just invert the probabilities and multiply them. You had a .170 chance on the turn, and a .174 on the river. By inverting, I mean subtracting them from one. Now we've got .830 and .826! Multiply and get .686! That's our chance of NOT hitting our card at all. So, invert it again and get .314, or 31.4%.

Example #3 "Top two pair"

THE POCKET

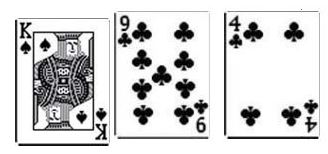
Play Texas Holdem Online Professional Guide 004

THE FLOP

Play Texas Holdem Online Professional Guide 004

You get dealt a King of Diamonds and a Nine of Hearts. The flop is looking' pretty good for you with a King of Spades, a Nine of Clubs, and a Four of Clubs. Top two pair!

Lesson 1: What are my chances of getting a full house on the turn?

To get a full house, you need another King or Nine to pop up. There is two of each left in the deck. So, you've got 4 outs. After the flop there's always 47 cards unaccounted for. 4/47 is around .08 or an 8.5% chance of you getting the Full House.

Lesson 2: What are my chances of getting a full house on the river?

If it didn't happen on the turn, your chances usually don't change all too much, but let's check. You've still got 4 outs and now 46 unseen cards left. 4/46 is about .087 or around an 8.7% chance of hitting it on the river. A .2% difference.

Lesson 3: How about the chances of getting the boat on the turn OR the river?

Like the previous examples, to figure your chance of something happening on multiple events, you need to calculate the chance of it NOT happening first. On the turn it won't happen 43/47 times. On the river it won't happen 42/46 times. 43/47 is .915, and 42/46 is .913. Multiply them and get .835, or 83.5% chance of it not happening. Invert that and you get a 16.5% of getting at least a full house by the showdown.

Lesson 4: What do you mean by "at least" a Full House?

Since we figured the chances to NOT get dealt a full house, the chances are built in if the turn and river are two Kings, two Nines, or a King and a Nine. If you are dealt two cards both of either King or Nine, it'll be four‐of‐a‐kind and not a King and Nine 33% of the time. Think of it as being dealt one card then the other. What are the chances of the first card matching the second? Whether it's a King or Nine, there will be only one unaccounted for, but two of the other. That's 1/3, or 33%.

Lesson 5: Then what are my chances of getting four‐of‐a‐kind?

This one requires a little more thought. It doesn't matter which card we're hoping for. We need to first get a full house on the turn. According to lesson #1, the chance of that happening is.085.

The chance of getting the same card we got on the turn is 1/46. There's only one out, and the usual 46 unseen cards. 1/46 is around .022, or 2.2%. Multiply the two probabilities (.022 X .085) and get .002 or one‐fifth of a percent. It will be Kings half of the time and Nines the other half Is this making any sense? If you really want to be a master of calculating odds, you need to see these calculations in action, over and over. Like anything else, practice makes perfect. In online games especially with very few if any tells (shown cards), statistical knowledge becomes the main factor when choosing whether to bet, call, or fold.

If you do have a hand that you know can't lose – you have the nut.

Bet like crazy.

While there is a lot more to Texas Hold'em poker than this ‐this should open your eyes to more things about the game of poker than just the cards and their statistics.

Yes, You DO need to know your general chances of pulling what types of hands ‐ but if you learn to study your opponents, they will tell you their hands and you'll be able to beat them without even knowing yours.

RETURN ON INVESTMENT (ROI)

When the stakes required to play a game of Texas Hold'em increase, there is not a proportional increase in the average winnings or money flow because most players, especially at the start of play, play tighter at higher stakes.

Here's how that works.

Higher stakes cause players to be more cautious. Pots do not grow proportionately as the stakes and blinds increase. Your return on investment will therefore decrease as the minimum blind goes up.

Max Bet Pot Size
$ 2 Max 28 - 37
$ 4 Max 25 - 35
$ 6 Max 20 - 22
$ 10 Max 10 - 28
$ 20 Max 6 - 7
$ 50 Max 12
$ 60 Max 7.6
$ 100 Max 6.11
$ 200 Max 5.5

Most major online casinos release data on hands played (for a price) on a regular basis. A recent study (June 2004) from one of the largest online casinos, based on several million actual hands of Poker played, revealed that the return on investment varies quite a bit based on the maximum bet.

In the $2 games, the value of the winning pot varied from 28 to 37 times the Big Blind (BB), the most you would have to invest to see the flop (short of raises). The average pots were in the $60 range. With the right cards, you could expect a return of 3000% on a winning hand.

As you can see in the chart above, this ratio falls as the Blinds go up. In the $200 game, with pots averaging $600‐1200, the ratio averages 5.5:1. Sure, greater overall winnings ‐ but much greater risk based on the investment you have to make to see the flop.

Also notice the volatility or variance of this ratio. On the high stake's tables, play is very tight and often passive, so the ratio remains very narrow – pots are predictably 5‐6 times the Big Blind. At the smaller stake's tables, there is considerably more volatility, indicative of a lot of looser players and more aggressive playing styles.

The $1/$2 tables are the loosest with pots ranging from 28‐37 times the Big Blind.

Are Low Stake Tables Faster?

Not necessarily. Texas Hold'em is the king of fast play. Several $1000 plus pots were played in less than a minute and ranged as long as 6 minutes, the same range for the small stake tables. Over all, the average length of an online Poker game today is just over one minute or 50‐60 hands per hour.

In higher stakes games, one thing is quite clear. There are a higher percentage of tighter and aggressive players at these tables than at the small stake games. That means there are more sharks at the big tables and a much better chance that you will be one of the fish. The smart thing to do here is to say away from these kinds of tables.

Given the fact that the return on investment is lower at the high-stake games, that the average level of play is much more aggressive and that a much larger stake is required, there is very little opportunity to be a consistent winner on tables with $50 and up blinds.

Insider Tip: "All of the recent research points to $5/$10 Limit tables as ideal combination of risk and reward."

FACT!

When the average loose gambler loses, he or she keeps on playing in an attempt to recover the loss. This is irrational and unplanned play and can be very expensive.

On the other hand, when most innate gamblers win, they forget all about their losses and conclude incorrectly that they have finally learned how to win ‐ or that their luck has finally changed. They express what is an irrational optimism at this point – a totally unfounded and undeserved optimism that keeps them in the game until they revert back to a losing streak.

Sharks exploit this irrational playing style in gamblers to generate a continuous income.

← Previous Next →
↑

Email: info@mttsports.club

© MTT Sports Club 2024